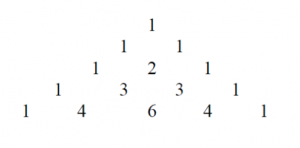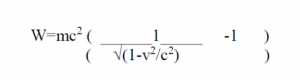“If you have ever studied geometry, you remember that by a course of reasoning, Euclid proves that all the angles in a triangle are equal to two right angles. Euclid has shown you how to work it out. Now, if you undertake to disprove that proposition, and to show that it is erroneous, would you prove it to be false by calling Euclid a liar?”

—Abraham Lincoln, Fourth Joint Debate at Charleston, 1858.

You readers of the American Mind live in a digital age and in an age of expertise. To greater and lesser degrees, the grandees, and to a large extent the rank and file, of media, literature, and the academy regard all knowledge as technical. Intellectuals today regard human beings as information and matter intelligible to human and artificial (think facial recognition) understanding according to the same methods as any other information or matter.

You also live in an age of political upheaval, here and around the world. Digital technology, while offering humanity efficiencies, power, and perhaps above all, powerful addictions, offers us little in the way of political advice. Without a framework in which to think about political judgments, political and legal systems are at risk of coming unglued. And if unglued, political and legal systems will need to be put back together. This cannot be done, except accidentally, without intellectual confidence that it is possible to think about nature, particularly human nature, coherently.

The 20th century’s greatest and most controversial abstract thinker on technology, Martin Heidegger, in his Being and Time (1927) and The Question Concerning Technology (1954) taught that all experience and interpretation is subjective and that technology and truth are, at bottom, indistinguishable. It is popular for high intellects of both Right and Left to embrace—or to hint at the embrace of—Heidegger’s thinking, or the thinking of those inspired by Heidegger such as Derrida, Foucault, and other post-modernists. Yoked to a single school of thought, they plow the tired soil in which the degenerate politics of the digital age grows. The alternative is classical rationalism.

Yet classical rationalism is no stranger to the fundamentals of the thought of Heidegger and post-modernists: human experience is bound by the interpretive structure of language and technology, which in turn alters experience, which then alters the interpretive structure again. Post-modern thought is alluring precisely because it is partly true, and it is easier to give in than to understand that it is only partly true.

Perhaps nearer to the truth is that the structure of language and technology has limits. Human experience, however subjective, has the unmistakable appearance of being grounded in an unchanging framework. This essay is an attempt to illustrate, in the spirit of classical rationalism and some aspects of modern science, the existence of such a ground.

All tribes can count to five. If we take this proposition as a given – and if we don’t we have insuperable problems – and these numbers imply a massive edifice of natural and invariable experience. All tribes or cities have some kind of political life. The limits implied by natural numbers serve as the beginning of wisdom about the limits of political life.

 

The Natural Numbers

The number “one” can be depicted as a single point:

                       

The negation of one, none, can be depicted as the absence of this point:

If a man can conceive of one, he can conceive of two:

          

And three:

          

And four:

          

And so on. Anthropologists have speculated that among the most primitive tribes, all have the ability to count to at least five, corresponding to the number of digits on a hand. If so then we can understand, without knowing them, that the world’s last uncontacted people, The Sentinelese, have the cultural, linguistic, and grammatical structures sufficient to count to at least five. When the Sentinelese expel an invader from their protected islands, they know if they have brought two, three, or five arrows.

Four, as depicted above, is a square number. The ancient Greeks referred to the product of a number multiplied by itself as “square” number, because, when depicted as equidistant points, such a number can be arranged in the shape of a square. If a man can count to five, he can, as depicted below, count five groups of five, or the square of five, 25, like so:

               

To go in one direction is to be able to return in the other, so our man who counts to 25 can also know the square root of 25 and, for that matter, the square roots of 16, 9, and 4. Further, if our man counts to 25, he can add four more, and have 29.

          

With 29 points before him and only a modest amount of curiosity, our man may easily discover that it is impossible to arrange his points in two or more equal groups of more than one point. He will have discovered prime numbers. The door is open to him to discover all nine prime numbers from 29 and 1, and to discover there are numbers that can be divided into two equal groups, even numbers, and numbers that cannot, odd numbers. We do not need to give our man too much credit to suppose he will figure out all prime numbers (other than the special case of 2) are odd.

These numbers, what we call “natural” numbers, correspond to invariable prescientific experience. Every man, wherever born, has an experience of one or none. Something “is” or “is not.” Every man, wherever born, experiences a multitude of things that he may categorize as the same—sticks, stones, shells, whatever. The numbers used to count such things are therefore commonly called “natural numbers”: they are those numbers whose existence anyone may discern naturally and without scientific study.

There is no imagining of intelligent thought without a notion, however vague, of one, and if one, of two, of even, of odd, of prime, and so on.

The Incommensurate Ratios

There are other rudimentary experiences that are likewise accessible to all human beings.

If our man takes two points and connects them, he may make a line segment. Fix one point of the segment and rotate the other end all the way around until it returns to its original place, and he has made a circle. With some study he can understand the ratio of the length of the line segment to the length of the curved line making the circle. He will discover this ratio eludes expression as a fraction of any two integers. It is incommensurate.

This thought of an incommensurate ratio can be taken and applied to other shapes.

A man may draw a square and discover that the length of the diagonal of a square, like the radius of a circle to its circumference, also cannot be expressed as a fraction of two integers. If a man can figure all this out, he can also figure out that if he takes a line and divides it into two parts such that the ratio of the two parts is equal to the ratio of the whole line to the larger part, that ratio also cannot be expressed as a fraction of two integers.

Our man will have discovered ?, √2, and φ, three very important numbers.

Triangles and Waves

Let’s return to circles.

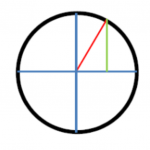
If our man takes a circle and bisects it twice so that it is quartered equally by straight lines through its center, these diametric lines will be perpendicular. If our man draws a radius to a point on the arc and drops a line segment parallel to one diametric line and perpendicular to the other, he will form a right triangle.

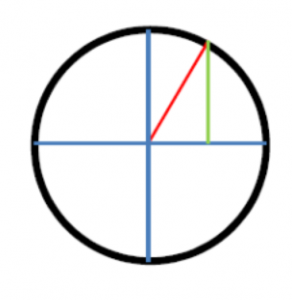
No matter the size of the circle, corresponding line segments may be drawn. Below is a larger circle and similar triangle.

No matter where the point on the arc of the circle happens to lie, for all similar triangles, the ratio of the opposite line to the radius (i.e., the hypotenuse) will be the same, as will that of the adjacent line and the hypotenuse and the opposite line and the adjacent line. If our man rotates the hypotenuse through the full arc and then through the entire circle, he will get a series of numbers expressing the changing ratio of the opposite side to the hypotenuse.

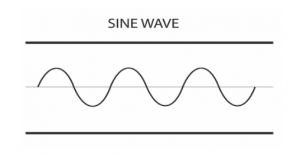
This may be depicted to make a pattern like a wave.

This information, a sine wave—because it is based on prescientific experience of a point or unit, a line or distance, a circle, and a triangle—is accessible to all human beings.

Now back to integers. If our man takes his integers and lays them out in a triangle, adding the two top numbers to get the next row, he will make a triangle of numbers as follows:

Perhaps he can discover some relationships among these numbers. Setting them out in a right triangle to the eighth row, he would get the following.

If our man looks at each column in the triangle above, the first column is a column of units, or ones. The second column is a column of natural numbers. The third column is a column of triangle numbers, the numbers one gets if one lays out points in increasing triangles like this.

The fourth row are tetrahedral numbers: triangle numbers in three dimensions. And so on.

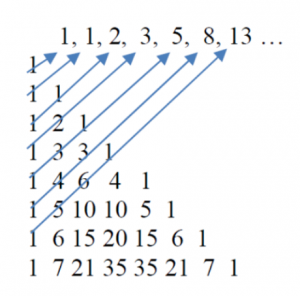
If our man takes the triangle above and add the numbers diagonally, he may obtain the following:

This sequence of numbers can also be derived by adding the two prior integers in the sequence to find the next. For this sequence, the ratio of any two adjacent numbers, as the sequence expands, converges on φ. This sequence is known as the Fibonacci sequence. Fibonacci numbers correspond in actual experience to a number of easily discoverable phenomena, especially where fractals are involved. For example, the spirals of a pine cone or in the seeds of a sunflower almost invariably come in sets corresponding to a Fibonacci number.

The triangle we have been discussing is known as Pascal’s Triangle, after Blaise Pascal. Blaise Pascal was not the first to discover Pascal’s Triangle. A number of people throughout history have noticed the relationship among numbers reflected in Pascal’s Triangle. In China, this pattern was known as Yang Hui’s Triangle. There are also ancient Indian manuscripts that depict this integer pattern.

Each row of Pascal’s Triangle discloses information about probabilities.

The value of each row is 2ⁿ where n is the row and the first row is 0. If our man has a fair two-sided coin, and he flips this coin 6 times, what is the probability that three and only three of the coin tosses will come up heads? The answer is found in the sixth row in the center place: 20. The probability of getting half of 6 coin tosses heads is 20/64 or 5/16.

Knowing the natural numbers implies knowing these probabilities, even if the knower does not yet know it because he has not thought it through.

Implied Knowledge

Or perhaps we might say, “if he remembered it.” The knower may not see the implications of what he already knows: this is a phenomenon explored in Plato’s dialogue Meno.

In Meno, Socrates leads a slave boy to see that his rudimentary knowledge of the relationships of a square implies that he also knows that a square with a side the length of the diagonal of the first square is double the area of the original square. The slave boy does not realize that he knows this until Socrates dialectically compels the slave boy to “remember” what he already knows.

The properties of mathematics Socrates demonstrates in Meno, as well as those demonstrated by Pascal’s triangle, have analogues in modern science.

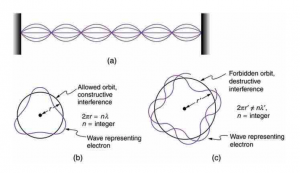
In the early 20th century, Niels Bohr examined the structure of the atom. Bohr’s data supported the notion that electrons orbit the nucleus of an atom in specific shells having specific energy states. An electron can descend one electron shell, emitting a single photon of a certain wave length. Conversely, if the electron absorbs the energy of a single photon, the electron becomes “excited” and moves to a higher electron shell.

The changes in electron orbit and energy are quantal: an electron cannot be found in between electron shells. This is the origin of the name “quantum mechanics.” Quantum mechanics led much of the world—still leads much of the world of popularized philosophy—to doubt the existence of a fixed underlying reality in nature, a return to Heraclitus’ all is flux and Parmenides’ all is one, stopping at Heidegger on the way.

Bohr had no explanation for the behavior of electrons in his model of the atom. It was enough that the data unequivocally supported this and predicted the physical behavior of the atom.

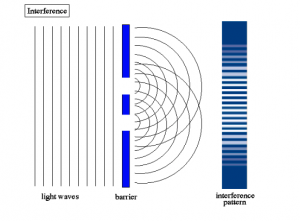
The French physicist Louis de Broglie studied the Bohr model of the atom in his Ph.D. dissertation, reflecting upon the behavior of electrons. Any particle smaller than a certain size (the “Planck length”) behaves like a particle and like a wave—not a wave you would find in the ocean, but a wave of local probability. Broglie reasoned that the mechanism by which electrons inhabit only specific shells might be a function of wave cancellation. That is, when the peak and the trough of two intersecting equal waves come together, they cancel one another out.

This behavior had been observed in photons using the famous “double slit” experiment, in which light photons are projected through two slits. Those photons which intersect cancel one another out, resulting in a counterintuitive pattern of strips of light where one once expected a uniform distribution of light.

Applying this principle to orbiting electrons, Broglie described precisely the fundamentals of the Bohr model of the atom. An electron could only occupy an orbit in which a whole number of waves equaled the circumference of the orbit. That is, the location of the orbit shell was r from the center of the atom, where 2?r equals an integer multiplied by the wavelength of the electron.

The mathematical description of wavelength of an electron employs a sine function: the changing ratio of the opposite leg to the hypotenuse of a triangle inscribed in a circle as described above under the heading Triangles and Waves.

In other words, what our man discovered about triangles, circles, and changing ratios gave him some implicit knowledge about the behavior of electrons. Aspects of quantum mechanics are described with great accuracy using concepts implied in integers, incommensurate ratios, circles, and triangles, which are accessible universally, even to our primitive man who counts only to five, based on common prescientific experience.

Prescientific Experience

Prescientific experience encompasses more than just integers and basic shapes.

From our earliest moments, human beings have basic common experiences. One such experience is “if-then.” “If-then” is a conditional statement which is connected to the experience of causation.

We learn, probably in a highchair, that if we push a bottle of milk off the edge of the platter it falls to the floor. Parents know of the great excitement inspired by these repetitive developmental experiences. The experience leads to an understanding of causation. As we are taught language, this understanding of causation is captured in conditional clauses: “If I push the bottle off the edge of the platter, then it falls to the floor.”

We also observe that events occur in a certain order and within a certain space.

There is a “before” and an “after”; there is also a “here” and a “there.” The sequence and location of events are recorded in memory, and if everything is working right, in the order and manner in which they were perceived by our senses. Time and space as concepts emerge, which are tied to our experience of conditionality “if-then” or causation. Causal events become more complicated.

We observe that when the bottle falls from the platter it never goes up, or sideways, but consistently moves in the direction of the floor. It appears to have an end toward which it tends to move. As we learn language, it reinforces this experience by enabling us to form and articulate concepts of becoming and change.

There are too many details of prescientific experience to examine them all here. These experiences can be unlearned, through superstition (the belief in magic) or materialism (the denial of the integrity of these experiences). But suffice it to say that, in daily life as in mathematics, all human beings experience certain fundamental things which may form a common ground of understanding across cultures.

This prescientific experience includes notions of a unit or one (object or thing), “if-then” (conditionality and causation), “before-after” (time), and “here-there” (space). Human beings render these abstractions into language and mathematics, a faculty the Greeks called logos.

While languages contain concepts that correspond to universal prescientific experience, they also contain conventions that correspond to particular political-cultural experiences, a feature from which mathematics is largely free. As a consequence, when literature is translated into other languages, some meaning is lost where the concepts in one language do not exist in the other. The Inuit are said to have many words for snow, and only a few words for bargain. Americans have many words for bargain, and only a few words for snow. Americans and Inuits have a different culture.

Mathematics is largely free of this because it is grounded in the fundamental concept of a unit and of units. These concepts continually correspond to experience such that math cannot be easily corrupted without destroying its intelligibility. Language, on the other hand, can be corrupted fantastically, and will still be understood by the people who share the culture which is the ground of the language. Consequently, mathematics is often regarded as a universal, and trans-cultural, language.

Special Relativity and Non-contradiction

In his 1905 paper, On the Electrodynamics of Moving Bodies, Albert Einstein addressed known problems in electrodynamics. That paper formed the basis of what would become his famous theory of relativity.

Einstein was very modern in his thinking. He reserved his admiration for philosophers such as Ernst Mach and David Hume, who held that causation was entirely a psychological phenomenon in the human species, not an objective feature of the outside world. Einstein generally rejected assumptions about the validity of prescientific experience. Yet, Einstein’s rejection of prescientific experience was perhaps less than thorough: his own demonstration of the relationships in space-time relies on an appeal to just such an experience.

Einstein wrote in Electrodynamics that the problem of a “luminiferous ether” or a “light medium” as a concept to explain the observed upper-bound of the speed of light in a vacuum, c, had its roots in an erroneous assumption about time and length. Specifically, proponents of the “light medium” assumed that time and space are uniform across frames of reference. Einstein’s model of special relativity maintained that c is the same for all observers, such that, no matter the frame of reference, light will, from the prospective of any observer, propagate outward at the rate of c.

As a result, a hypothetical driver of a car moving at near the speed of light flicking on his headlights would observe light propagating away at the rate of c. A stationary observer in another frame of reference would observe the car moving at near the speed of light and would observe light from the headlights propagating at the rate c without any addition of velocities (i.e., the speed of the car plus the rate of c, the speed of light). The difference, Einstein speculated, was explained by a changing experience of time and length in the alternate frames of reference.

While special relativity rejected (in part at least) prescientific experience with respect to “before-after” and “here-there,” Einstein nonetheless relied on an argument based on observed prescientific experience to argue, logically, that the c was the upper bound of any displacement. He wrote:

Thus, whereas the Y and Z dimensions of the sphere (and every rigid body of no matter what form) do not appear modified by the motion, the X dimension [the direction of translation] appears shortened in the ratio 1: √(1-v2/c2), i.e., the greater the value of v the greater the shortening. For v=c all moving objects—viewed from the “stationary” system—shrivel up into plain figures. For velocities greater than light our deliberations become meaningless.

A few pages on, Einstein makes the same sort of argument with respect to the mass of an accelerated body.

Using the formula

Einstein argued: “Thus, when v=c, W becomes infinite. Velocities greater than that of light have—as in our previous results, no possibility of existence.” [Emphasis added].

This sort of argument is fundamentally similar to that used by Socrates in Meno to demonstrate what a slave boy implicitly knows about squares.

Certain contradictions may be considered impossible to reconcile with the experience of a square or, in Einstein’s case, length or mass. Imaginary length and infinite mass is incompatible with certain prescientific experience, and therefore impossible.

This same principle, by which contradictory propositions are discarded to formulate a hypothesis, is a ground axiom, or first principle, of Aristotle’s metaphysics.

Binary Numeric and Logic Systems

Returning once again to integers: we count in base ten generally, and it is widely assumed that we do so arbitrarily on account of the common experience that human beings have ten fingers. It is, in fact, only convenient but not necessary for human beings to count in base ten. We may count in base two, in 1s and 0s. To count in binary, we start with 1, then 10, then 11, and so on, as follows:

Reminding us of Pascal’s Triangle (suggesting also an interrelatedness), every 2ⁿ corresponds to the expansion of a binary numeric system as follows: 10(2), 100(4), 1000(8), 10000 (16), 100000 (32), 1000000 (64), 10000000 (128).

Leibniz, a Sinophile, observed that the Chinese symbols recorded in the ancient text of the I-Ching were in fact a binary system of counting. Building on this, Leibniz speculated that a binary counting system could be used to incorporate a system of logic into a numeric system. In so doing, he laid the ground for modern computing.

Using 1s and 0s to represent true or false statements, Leibniz showed it is possible to develop truth tables that incorporate logic functions. 1s and 0s can be represented by any gate that can be in an open or closed position, which makes binary logic and numeric suited to electric switches which can be in an on or off position. With the miniaturization of transistor circuits on silicon, we have the modern computer, like the computer on which I write this. What I have written—and what you are reading—can be and is represented, and manipulated, using only 1s and 0s.

Numeric logic does not have to be limited to binary logic.

Russian computer designers in the 1970’s experimented with ternary logic systems. Instead of an on-off switch, this system used -1, 0, and 1 corresponding to a negative charge, no charge, and positive charge on a three-way gate. In the ternary logic functions -1 represented false, 1 true, and 0, a third state, was designated “unknown.” This computer system, known as the Setun, ran certain processes more simply and therefore more quickly than could a binary computer.

However, there were no functions the ternary logic could perform that could not also be performed using a binary logic system. Ultimately, the design was abandoned as impractical given that miniaturization and processing speed of binary logic chips simply had eclipsed any design advantage.

The modern miracle of the digital age is quite simple. Binary logic chips are inextricably rooted in a prescientific experience of a single unit of something or none of it.

With that we are brought full circle to one.

Say What Again: Math or Biology

One, a unit of something, raises the question, “one what?”

Plato, as is well known, developed a metaphysics in which “oneness” and “twoness” and “evenness” and “oddness” each had a Form or Idea, an abstraction that constituted an actual reality as a thing in itself. Experience for Plato was a reflection or simulacrum of this abstract reality.

Thus, for Plato, the question of “One what?” was answered by the noetic Form or Idea. One apple has its being because of the Form of “oneness” and the Form of “apple.” Any given one apple, experienced through the senses as in everyday life, is merely an imperfect reflection of the actual, perfect One Apple.

Plato imagined these relationships climbing a ladder of mathematics, and he consequently required mathematics as a prerequisite to membership in his school, the Academy. Clues as to this mathematical account are strewn throughout his important works.

For example, the simile of the divided line in Republic is structured around a line divided in half in and half again so that the proportions of the first halving are the same as the proportion of the next halving. Plato is not explicit, but this reminds us of φ, the result obtained when a/b=(a+b)/a or the convergence of the Fibonacci sequence. The top portion of the line is the contemplation of the Forms or Ideas as pure abstractions, and the second part of the line is mathematics.

Plato’s Republic is often taken as a description of an actual city—indeed Aristotle, Plato’s most famous student and critic, knocks Republic in a way that suggests, perhaps ironically, that the dialogue describes a real city rather than an abstraction. Republic, however, exoterically at least, is a discussion of justice and a rebuttal to a difficult argument posed by Thrasymachus, a leading sophist of the time, that justice is the interest of the stronger.

The rebuttal Socrates makes in dialectical manner turns out to be a mathematical proportion, like the constancy of ratios in two similar triangles or in circles of any size. The city is organized into philosopher kings, guardians, and traders and tradesmen based on a deception that there are gold, silver, and bronze people and, similarly justice, the psyche of a just man, is organized such that, roughly speaking, reason (logos) controls anger (thymos) which in turn controls desire (eros).

The question “one what?”, answered as an abstraction that is only accessible to philosophers, renders common sense experience a mere shadow of reality. This may be intoxicating, but it has shortcomings.

Thankfully, the question “one what” can also be answered by the experience of biology. I mentioned above the rudimentary phenomenology of a baby in a highchair pushing a bottle off the edge of the platter and watching it fall. The baby perceives an object or thing which it unifies into an abstraction. If mom takes the bottle apart and pours out the milk, the thing loses its integrity. But conceiving of the bottle as a thing, the milk, the container, and the lid are unified into a single thing, a unit.

This is done noetically by the thinker, in this case, a baby. After limited experience with bottles, our baby—if he develops normally—comes to understand that there are many bottles, no two of which are exactly the same, and an infinite number of possible bottles. This thinking expands to other familiar things such as chairs, tables, toys, etc.

If we imagine this baby’s experience, we can suppose that initially there is no real distinction for this baby between what is alive and what is dead: everything is alive. This obliterates, of course, the distinction between alive and dead, and everything is also equally dead.

As experience shapes thinking, this thought develops into “things that move are alive”: mom is alive, the dog is alive, the cat is alive, and then the terrifying classic error, the vacuum cleaner is alive. As prescientific experience accumulates, our baby, who is probably not a baby anymore, starts to distinguish between things that are actually living and things that are dead on a more sophisticated basis than “things that move.”

“One what?”—a thing or things become understood by virtue of the experience of them as a unity. And this is most evident in a living thing. The living things are distinct from their surroundings in a way that other material things are not. The common sense experience of a dog renders it distinct from the experience of other things.

For example, returning to the bottle, the bottle has no easily discernible existence as a bottle apart from how the baby or someone thinks about it. On its own, is it easily distinct from its surroundings or its contents, or is it a heap of plastic, milk, and rubber? If I pour out the milk and use the bottle as doorstop, it is a doorstop.

As a bottle or a doorstop, and not a heap of plastic, milk and rubber, it is an artifact the existence of which is a function of an artisan, the intention of a thinking human being. The same cannot be said of the dog, which has its own internal moving principle, so long as it is alive. And when it is dead it is no longer a dog. But when it was alive, its unity as a dog does not appear to depend on how a thinker thinks about the dog.

The above is a highly truncated account of Aristotle’s concept of a hylemorph. Aristotle resolves the problem of “one what”—the problem of form—such that the common sense experience of form corresponds to its underlying reality. A dog is only a dog if it has all its necessary parts—if it is missing a leg it is a three-legged dog—but if it is dead it is not a dog but a dead dog. The essence of a living thing, the form, is its psyche, which in animals is a locomotive principle and a metabolic principle, and in a plant it is a metabolic principle (although plants do move, just not terribly perceptibly).

This idea of form and matter in biological things serves as a framework for understanding all other things, attributing a form that is either internal (e.g., a psyche) or external (e.g., the intention of a human being).

This incorporates further a four-fold idea of causation which is inherent in prescientific experience—whether you are Sentinelese or an infant New Yorker—material, efficient, formal, and final cause. The baby senses the matter (material cause). The baby perceives the matter is in the form of a thing—in the case of our baby, a bottle (formal cause). The baby pushes the thing to the edge (efficient cause). The thing falls, tending to fall to the ground (final cause). The expansion of experience continually reinforces this, e.g., a child grows a bean sprout and observes matter and form becoming a plant.

Modern science is not at ease with this account. The attribution by induction of form and final cause to the experience of things is considered naïve, a projection onto experience by human thought that has no underlying truth to it. Indeed, the radicalized modern scientific account rejects even bare causa efficiens as wholly psychological. All things are dependent on thought.

Yet as the discussion above shows, in the case of Einstein, the argument he made for his hypothesis—which had not been tested when he made—depended on a partial validation of prescientific experience and a rejection of contradictory notions. In the case of biology, reductionist biology continually must make allowance for the existence of living things distinct from their surroundings, distinct from things that are dead, and distinct from dissimilar living things (things of a different species).

Otherwise, what would biologists study?

Without such indulgence—a suspension of the rigor of reductionist materialism—biology is irreducibly unintelligible.

The Problem of Modern Orthodoxies

Modern science has two orthodoxies which dominate its thinking. One is the falsification principle of Karl Popper, and the other is the revolutionary principle of Thomas Kuhn.

At the risk of giving serious thoughts short shrift, Popper’s falsification principle provides that a scientific theory must be falsifiable. Once falsified a scientific theory is no longer valid. This is based on a rejection of inductive reasoning of the kind described above with respect to biology and hylemorphs, a rejection Popper shared with Hume.

Kuhn’s The Structure of Scientific Revolutions divorces scientific understanding from a notion of objective truth and grounds it instead in a consensus of the scientific community. A paradigm such as the Newtonian fixed inertial frame of reference is not modified by special relativity and general relativity, but overturned in a revolution resulting in a new scientific consensus which in time is likewise overturned.

Kuhn and Popper confine scientific thinking to a reigning orthodoxy, one which is, incidentally, at odds with the common sense experience of its adherents.

Do not take my word for it.

Leading physicist Carlo Rovelli has commented on it quite ably in a 2014 paper called “Aristotle’s Physics: A Physicist’s Look.” Rovelli is explicit that re-examining Aristotle is a means to liberating thought in physics, which has become constrained by the very doctrines of Kuhn and Popper that were intended to liberate science from inductive reasoning. Indeed, devotees of Popper and Kuhn must puzzle over authoritative claims about falsification and the structure of revolution when the authority of these claims must be exempt from their own thought.

Thus, by its own account of itself, modern natural science does not think it should be open to considering its results cumulative. It needs, perhaps, to engage in a little remembering.

Aristotle, in Book III of Metaphysics, rebuts the idea of all truth as dependent on thought on the grounds that no one actually acts as if that were true. A man walking from one town to another does not behave as if that act were psychological. Further, Aristotle argues, he who thinks four is five is not equally wrong with someone who thinks it is one thousand. It is possible for two views to be wrong and one of them to be “nearer to the truth.”

Were modern natural science to suspend its commitment to its orthodoxies, might it illuminate more rather than less?

Newton can give an account of physics that is correct within his domain of experience without being wholly falsified or overturned in a structural scientific revolution. Falsification and revolution closes off the sound thoughts of the past as much as it may liberate the thoughts of the future.

But it is often necessary to reconsider past opinions in order to critique the current opinions of science.

For example, in Appendix V of Relativity: The Special Theory and the General Theory, Einstein repudiated in part his views on the real existence of space, invoking classical thought: “Why is it necessary to drag down from the Olympian fields of Plato the fundamental ideas of thought in natural science to attempt to reveal their earthly lineage?” he asked. “Answer: In order to free these ideas from the taboo attached to them and to achieve greater freedom in the formation of ideas and concepts.”

Rather than jealously guarding its church of twin self-referential doctrines (Popper and Kuhn), modern science might tolerate a third, liberating idea of science as cumulative understanding which proceeds nearer to, and necessarily sometimes further from, the truth about experience. (e.g., String Theory, a mathematical multi-dimensional exploration of relativistic and quantum phenomena which posits multiple dimensions, may well be further from the truth than the unreconciled world of Einsteinian relativity and quantum mechanics).

Modern science certainly acts and speaks as if science proceeds cumulatively, even if it doctrinally refuses to confess that it thinks that way.

The genius of Aristotle’s account is not that it is authoritative. Rather, his account of nature is flexible and, importantly, consistent with the actual experience of it. The examination of experience does not, as in the case of Plato or worse, Hume, have the effect of creating a growing and increasingly contradictory gap between prescientific and scientific experience. The essential prescientific experience can survive examination.

This is important because one cannot discard all prescientific experience without requiring an exemption from one’s own thought. One cannot speak intelligibly in terms of “objects” or “things,” “before-after,” and “if-then” in order to maintain that these prescientific concepts are fundamentally false.

One can ask, does excessive confidence in unintelligibility foster sound consensus—or superstition?

Douglas Hofstadter in Goedel, Escher, Bach: An Eternal Golden Braid (1979), an iconic account of artificial intelligence, makes almost no reference to Aristotle. Yet Hofstadter’s account of intelligence contains some themes that are strikingly similar.

Foremost among these are the notion of intelligence as recursive (analyzing experience, including itself, in a repeating application of a routine) and the possibility that intelligence may be isomorphic. By isomorphic Hofstadter means to say that the structure of human thought is similar to that of the whole external universe itself.

Hofstadter does not commit to human thought as isomorphic. Hofstadter is open to the idea that it is possible that human thought is arbitrary, a tangle of conventions circumscribed by the limitations of human beings which perceive and interpret arbitrarily.

This latter idea, however, obliges one to question whether one, a unit, is anything other than a projection of the human mind, as is two, odd, even, and prime, incommensurate ratios, and the similarity of geometric figures. This crumbling of prescientific experience renders every part of experience unintelligible.

On the other hand, the correspondence of one and two, and even, odd, and prime, and incommensurate ratios such as ?, √2, and φ, and Pascal’s Triangle to actual experience, including things that we do not experience until after we form these fundamental concepts, ought to give us pause as we march toward chaos.

Let us grant that our thought is in some part mistaken, like the man who thinks four is five who is not as mistaken as the man who thinks it is one thousand. Can we dismiss the idea that the structure of human thought, running its routines on an electrically and chemically active mass of biological matter (the brain), is similar in structure to the structure of the whole?

We cannot do so, at least not easily and not without causing a host more problems than we solve.

Natural Right

Such problems are not just problems for mechanical science but are problems for political well-being.

Our regime, the regime of the United States, is grounded, in part, on an abstraction similar to the abstractions discussed above, that “all men are created equal.” Disputes over the meaning of this claim are at the heart of the most intense fury of American politics. One what? What is a man? In what sense is he equal? What is his happiness? How should a statesman know what to do and how is he best advised?

The answers to these questions are likely to be found in the actual experience of politics in the light of an examined understanding of the unchanging ground of this changing experience.

Such examination is still open to us. The path forward need not be blocked by materialist orthodoxies, which are now causing significant deficiencies in science itself. But we cannot deny or ignore reality: serious investigation of the meaning and truth of politics, human equality and the natural rights and duties that flow from our nature has been largely blocked for the better part of a century.

If we are to answer the looming questions concerning political and natural right in the American regime, we must first establish that answers to those questions are possible. Many intelligent and educated people, as well as everyone else, have long been taught they are not, and that such questions are meaningless. This is because they have adopted the thought of modern science critiqued above.

This means re-establishing understanding of the connection between prescientific knowledge, e.g., such as the seemingly simple achievement of counting to five, and larger scientific understanding; quite literally it means exploring the link between the digits on one’s hand and the digital. It requires demonstration based on reason, not revelation, that can speak to both what everyman knows and what modern man knows best. The innovations of science over the ages and now do not falsify truth, but reveal it. We just need to know where to look and what to remember about what we already know.