The foundational truths are written into our experience. We just have to remember them.
A Cryptic Reply to Robin Burk

There is no logical way to dismantle the foundations of logic.
“That is because you are wise, Thrasymachus,” Socrates said. “Hence you know quite well that if you asked someone how much twelve is and in asking told him beforehand, ‘See to it you don’t tell me that it is two times six, or three times four, or six times two, or four times three…’” — Plato, Republic 337b
Robin Burk is wise, holding a PhD in artificial intelligence, machine learning, and information theory, as well as an MBA from University of North Carolina, and a bachelor’s degree from St. John’s College. Burk has objections, strongly felt ones, to the manner in which Glenn Ellmers characterized questions regarding teleology and to the manner in which I examined natural numbers and prescientific experience as they may relate to a nature by which we might know something about politics.
Burk claims that Aristotle’s method of examination of experience and of the ordered structure of the world “[f]ounders precisely on the results of looking closely at our world and ourselves. Those who would argue for a polity and society grounded in natural rights are also failing precisely because they have not absorbed what science and mathematics have uncovered in the last century or so.” This conclusion squarely rejects the existence of principles “applicable to all men at all times,” principles at the heart of the Claremont Institute’s defense of statesmanship.
There is a feature of Burk’s contribution to this discussion, however, which is indeterminate. That is, I cannot tell whether Burk believes that science has uncovered something which finally, and thus dogmatically, dispels the basis of natural right, or whether she feels such a basis may be simply hidden from view, either by virtue of certain opinions or by the actual experience of it.
Concealment
Hiding from view is a behavior of many natural things. The tiger, the octopus, the chameleon, many animals of the natural world use concealment offensively or to protect themselves from danger. Human beings use concealment as well. In political and philosophic writing, writers sometimes conceal their views with esoteric messages with a view to their safety and the safety of those who might misapprehend their teaching. In other communications, in business, politics, and in war, the concealment of speech itself can be paramount.
One method of concealment is to say two or more contradictory things directed at a specific audience able, or unable, to discern which of the two or more communications is the intended communication. In the middle of the Second World War in a public space where it was assumed that German spies were present, General Patton blurted out, “I’ll see you in Calais!” This, it was assumed, would be reported in Berlin and lead to confusion as to the precise location of the coming invasion of Europe, causing the German defenders to misapply their defensive resources.
Another method of concealment is encryption. While encryption is everywhere today in the digital world, encryption has been around since the beginning of speech or logos. One thing to know about encryption is that no code is indecipherable. Given time and resources even the most complex encryption can be broken. Encryption works on the principle, generally, that by the time the code is broken, the information will be stale.
An early form of encryption involved coiling a strip of paper or leather around a rod of a certain diameter. The message to be encrypted was then written on the coil on the rod. Removed from the rod the message on the strip was a jumble of fractional marks, decipherable easily if one only knew the diameter of the rod.
Another form of encryption is known as a “book cipher.” A book cipher works by two parties, A and B, each possessing matching copies of a certain book, like the same edition of a King James Bible. The code is then delivered by A to B as a string of numbered pairs, where the first number represents a page number of the book and the second number represents a specific word on the page. The first letter of that word is a letter in the coded message. When all the numbers are deciphered, a complete message is revealed. Such ciphers are painstaking to code and to decode, at least manually, even when you have the key (the book).
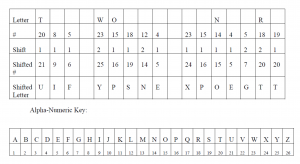
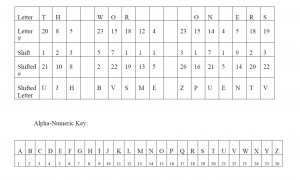
Another type of code is a letter shift code. Below are three meaningless collections of letters.
A. EQHX AIJT LOZURVXVN KBYL E DIQXYFO NMUB
B. UIF YPSNE XPOEGTT
C. UJH BVSME ZPUENTV
Or are they meaningless? It depends on what we do or do not know about them. In the Second World War, letter shift codes were used extensively to protect information. Germany used the Enigma Machine for its important communications. Thanks to the brilliance of Polish and British agents, particularly Alan Turing, the Enigma Machine encryption was broken, and the Allies were able to read most all sensitive German communications. The United States also used letter shift codes.
In order to hamper the deciphering of letter shift codes, a common practice was to begin any coded transmission with some nonsense letters. This was done because if the codes were sent using customary openings and closings—such as “To General MacArthur” or “From General Eisenhower” —these obvious patterns might have given enemy code breakers enough to determine the basis of the letter shift and to use that to decipher the balance of the message.
In a famous incident in the Second World War, Admiral Nimitz sent a communication to Admiral Halsey regarding his Task Force 34, which during the Battle of Leyte Gulf had been lured north by a Japanese deception. Nimitz wanted to know Halsey’s location in order to determine if Task Force 34 was in a positon to assist Admiral Kinkaid’s desperate position near Samar. The message was:
WHERE IS, REPEAT, WHERE IS TASK FORCE THIRTY FOUR?
This message was transmitted with prophylactic nonsense words at the beginning and the end.
TURKEY TROTS TO WATER GG FROM CINCPAC ACTION COM THIRD FLEET INFO COMINCH CTF SEVENTY-SEVEN X WHERE IS RPT WHERE IS TASK FORCE THIRTY FOUR RR THE WORLD WONDERS
The deciphered message was delivered to Halsey but the radio room inadvertently included the meaningless text THE WORLD WONDERS at the end. Halsey thought these words were a harshly critical message from Nimitz. Halsey had a breakdown in response to the perceived humiliation and delayed a full hour before turning his task force around to come to the aid of Kinkaid, arriving too late.
Carelessness has consequences in messaging, especially encrypted messages.
Sequences and Letter Shifts
Sequences can be used for a simple letter shift code. In mathematics, a sequence is an enumerated collection of elements. If party A sends an encrypted message to party B using a sequenced letter shift, so long as party B knows the sequence, party B can know the changing letter shift. Knowing the changing letter shift, party B can take the encrypted message and decode it. If a person intercepts the message and does not know the sequence, the encryption can take some time to break.
There are all kinds of sequences, and sequences have all kinds of properties.
A popular sequence I discussed in my essay, the Fibonacci sequence, has the interesting feature that as it expands the ratio of each of the last two consecutive digits of the sequence converge on φ.
The number φ happens to show up in quantum mechanics, in Hardy’s variation on the Einstein-Podolsky-Rosen experiment. In this experiment quantum mechanics predicts that a certain event will occur with a probability of 9.017%, which is g5. g (0.61803) is the reciprocal of φ, and is the ratio of the longer part of a line to the whole line where it is the same as the ratio of the shorter part of the line to the longer part of the line. Local indeterminacy is describable in this instance using a sequence of natural numbers.
Curious indeed.
In any event, the Fibonacci Sequence is derived by starting with 1 and then adding for each subsequent digit the last two digits in the sequence, expanding infinitely. 1, 1, 2, 3, 5, 8, 13, 21, 34… and so on.
Another fascinating sequence is known by at least three names: Conway’s Sequence, the Cuckoo’s Egg Sequence, and the Look-and-Say Sequence. The first name comes from John Horton Conway, a mathematician. The second name comes from a famous book on cryptography and hacking by the title The Cuckoo’s Egg, where the sequence appears as a puzzle in cryptography. The puzzle is to identify the next number in the sequence without knowing the method used to derive each prior number in the sequence. The name Look-and-Say Sequence comes from this method. Start with a number, d, and then look and say the quantity of the number you see, and repeat. d, 1d, 111d, 311d, 13211d …
One of the things about the Look-and-Say Sequence is that at first glance it seems to be an entirely arbitrary arrangement. In part this is because it appears to be derived linguistically. However, the sequence expands the same way in any language, i.e., it does not matter what language you are using—Chinese, English, any language —to “look” and “say.” Conway spent a good part of his career studying the sequence and discovered every sequence decays into a number of series of “atomic elements.”
The Look-and-Say Sequence is interesting also precisely because it has the appearance of being totally conventional, much like Burk suggests the idea of a unit may be.
In any event, if you start with 1, the sequence unfolds as follows: 1, 11, 21, 1211, 111221. The letter shift in B above, UIF YPSNE XPOEGTT, is based on the Look-and-Say sequence. If you look the letter shift is the cumulated Look-and-Say Sequence seeded with 1 until the string is 15 digits.
There is no reason to use Look-and-Say for a simple encryption other than the fact that it is very easy to do. This is because the shift is never more than three (and the seed number, if not one). This is good enough at least for passing notes to friends in school, since, as I mentioned, all encryption can be and needs be is good enough so that by the time the cipher is broken the information is stale.
One could also use the sequence of primes, or, if you want to make it harder, the sequence of primes plus a letter shift of the Look-and-Say sequence. The letter shift C above, UJH BVSME ZPUENTV, is the sequence of primes (2, 3, 5, 7, 11, 13, 17, 19, 23) but starting with 1 (which is not a prime). I started with 1 because that conveniently, through the number 23, yields 15 digits.
To decode these simple ciphers all you need to know is the letter shift order, or the sequence, and work the illustrations above in reverse. I have left a few blanks for you to decipher for yourself.
From the above you can decrypt the phrase
THE WORLD WONDERS
which had been the cause of so much trouble on one day in the war in the Pacific.
Enigma
I mentioned the Enigma Machine above. Enigma was a letter shift cipher. But it was a lot more complex than the letter shifts I have described above.
It consisted of electronic rotors having 26 positions, each corresponding to a letter of the alphabet. Each machine came with five rotors, only three of which were used at a time. The rotors were combined with a plug-board with ten pairs of letters that could be connected. On any day the key thing to know was the settings that were to be applied to encrypt and decode a message: Which three of the five rotors, in what order, with what starting letter on each rotor, and what combinations to arrange on the plug-board (an extra flourish of German thoroughness). Each time a letter key was struck, the rotors mechanically rotated so the next letter would have a different letter shift than the prior one.
Taking the five rotors, the three rotor settings, and the plug-board, the Enigma Machine had 158,962,555,217,826,360,000 possible combinations. Yet this code was manually breakable. In fact, parts of messages had been decoded by hand at Bletchley Park in England before Alan Turing designed an analogue computer that could discover the settings by analyzing intercepted transmissions. The problem was hand decoding was far too slow. By the time the codebreakers decrypted the message the information was stale, tactically and strategically useless.
Turing’s computer could take a day’s encrypted message and by running the message through a series of reverse engineered rotors discover the settings for all messages for the day. Once the settings were known, all the intercepted messages made on that day could be decrypted.
And so the war was won.
Qubits and the Excluded Middle
158,962,555,217,826,360,000 is a fantastically large number. However, it is dwarfed by the permutations of possible encryption techniques that can be generated using modern computers. While no encryption is unbreakable, the question, again, is always how much time it takes to break it, and if it can be broken before the encrypted information becomes stale.
A conventional computer must run its efforts at decryption in a linear fashion, meaning one process after another, using its on-off gates, representing 1s and 0s. Even using networks, each node in the network is running its effort in a linear fashion, 1s and 0s, then more 1s and 0s.
A quantum computer has advantages. A qubit can be a 1 and 0 indeterminately, a two-state system version of the classical binary bit architecture. With a much smaller number of gates, which can be a 1 and 0 indeterminately, a quantum computer can run a much greater number of permutations, in a manner of speaking all at once, rather than linearly. Wow.
This is why when you read about quantum computing the alarmist reaction is that encryption, so important for politics, business, and above all war, is under threat. Quantum computing would crack the Enigma Machine, and all other classical encryption, like an egg.
But fear not, keepers of secrets. Quantum encryption is coming.
How this works is not as complicated as it sounds. Quantum mechanics is not magic, and should not be considered as such.
The two state quantum system by which a quantum computer works (in part) is known as superposition. Superposition is the ability of an electron (or other Planck-length particle) to either have no state or be in two states at the same time (it is not necessary to know which) until measured or observed (which is to say interacted with). Superposition is not new. Nor is the understanding of the local indeterminacy of Planck-length systems, like electrons.
I discussed this briefly in my essay when I discussed Broglie’s work explaining the mechanics of the Bohr model. That explanation is tied to a classical trigonometric function which—surprise—describes a lot of probabilistic quantum functions, such as the probability of the orientation of an atom leaving a rotated Stern-Gerlach analyzer. The indeterminate Planck-length world remains adequately described by concepts derived from very simple prescientific experience. And, get this, they are described this way, linguistically, across cultures. The people in China can understand quantum mechanics, and so can people across the ocean in Palo Alto.
The qubit logic functions, at bottom, on the tried and true classical binary logic of 1 and 0. Superposition simply allows a gate to do a lot more at any given moment because a gate can be in a position of neither 1 nor 0 or of both 1 and 0 (depending on how you think of it) at the same time. Burk warns that this has destroyed the “deterministic” logic of the Excluded Middle on which classical natural right rests.
Has she thought this through, given that the claim that an electron “is” superpositioned itself relies on the logic which Burk suggests has collapsed? What then does it mean to say the electron “is not” superpositioned? Just a linguistic vestige?
The difficulty arises in that in order to maintain this position the speaker must exempt themselves from their own thought.
Retreat Before A Horde
Burk says the lessons of the 20th Century can be summed up in terms of the failure of deterministic categories and logic, the increasing prevalence of complex adaptive systems in our lives (especially those that are networked), and the meta-nature of humans.
Like Thrasymachus, whose argument tends to rest on the claim that everyone knows that everywhere justice is the advantage of the stronger, Burk’s response is lacking in arguments not based on the authority of opinions.
She cites John McCarthy, Marvin Minsky, Nathaniel Rochester, Claude Shannon, Kurt Goedel, and Alfred Tarski. She cites Albert Einstein, Rachel Giora, Istvan Kecskes, and others unnamed who showed that we develop concepts and language over time. She cites transfinite numbers as proof of the incoherence of the idea of a unity. But she offers very little detail about what these authorities actually said, nor does she offer any independent analysis of the concepts themselves that one can sink teeth into.
This leaves one with the impression that one is being invited to retreat before this horde—living, dead, and transfinite—of authorities, who we are told unequivocally doubted their own existence, at least as they understood it on any day that they got out of bed, brushed their teeth, went to work, loved their loved ones, and despised their enemies.
One of the most amazing features of her argument from authority is that it makes absolutely no sense without assuming that each of McCarthy, Minsky, Rochester, Shannon, Goedel, Tarski, Einstein, Giora, and Kecskes is or was an actual thing, belonging to the general category of human being, who has certain qualities and advanced certain arguments, by categories of logic and supported by experience, which compel us to accept them as authorities.
It’s a case I fear she will not bother to make. I think this because it is a case no one can make, not without undermining oneself.
Perhaps her argument contains an encrypted assumption that we suspend the truth in order to tell it in a classical sense so it all holds together. Perhaps Burk will make the defense that this not her fault, but is a linguistic necessity, which she has transcended intellectually, but which cannot be explained within the web of those limitations. To rebut that, read my discussion of Al-Ghazali in my reply to Alex Priou: the enthusiasm the scientific world has for this idea may in fact lead, as it happened in the Islamic world, to the enervation of its power to deliver advances in science and technology, based on the old deterministic logic of “what happened before could happen again from the same causes.”
My essay began with an invocation of political causes which invite us to explore some of these basic features of ourselves and the whole. The most disturbing feature of Burk’s argument is that it is strikingly similar to that essence of the argument of Alexander Stephens in the Cornerstone Speech, which denied the natural rights foundation of the United States set forth in the Declaration of Independence, on the grounds that “These ideas…were fundamentally wrong.”
The reader should at this point have enough information to decrypt the balance of this reply.
The American Mind presents a range of perspectives. Views are writers’ own and do not necessarily represent those of The Claremont Institute.
The American Mind is a publication of the Claremont Institute, a non-profit 501(c)(3) organization, dedicated to restoring the principles of the American Founding to their rightful, preeminent authority in our national life. Interested in supporting our work? Gifts to the Claremont Institute are tax-deductible.
Notes on nature’s means to nature’s ends.
What is the Bedrock of Being? (A Reply to Alex Priou.)
Must the natural scientist become a political philosopher?
A Response to Glenn Ellmers and J. Eric Wise
What If Rights Have Gone Extinct?